Algebra
Exercises
The algebra qualifying exam is usually quite a time crunch so one of the best ways to study for this exam (and pretty much every written qualifying exam) is by going over a bunch of exercises and solving as many problems as you can find. I've collected a bunch of problems from many different resources for you to use. I'd like to give a huge thank you to Mike Pierce for providing me with a majority of these problems! If you have any other suggestions please let me know! A couple of us grad students are also currently working on updating a website, originally made by Alec Martin, where we can have a giant repository of questions for all of UCR's math qualifying exams. If you're interested, feel free to shoot me an email and I will try to keep you updated on this. In the meantime...
Standard Algebra Exercises — This is a list of those ubiquitous algebra exercises that pop up on many exams and are in most algebra textbooks. You should hopefully know how to solve all of these problems by the time you take your qual!
Harder Algebra Problems — These have more meat on them than the other exercises.
Here is the hierarchy of algebraic objects ranging from semigroups to fields. Each ellipse contains an example of its corresponding object strictly in its respective classification.
If you know good examples that you think are worthy and would like to see on this picture please let me know and I'd be happy to include it.
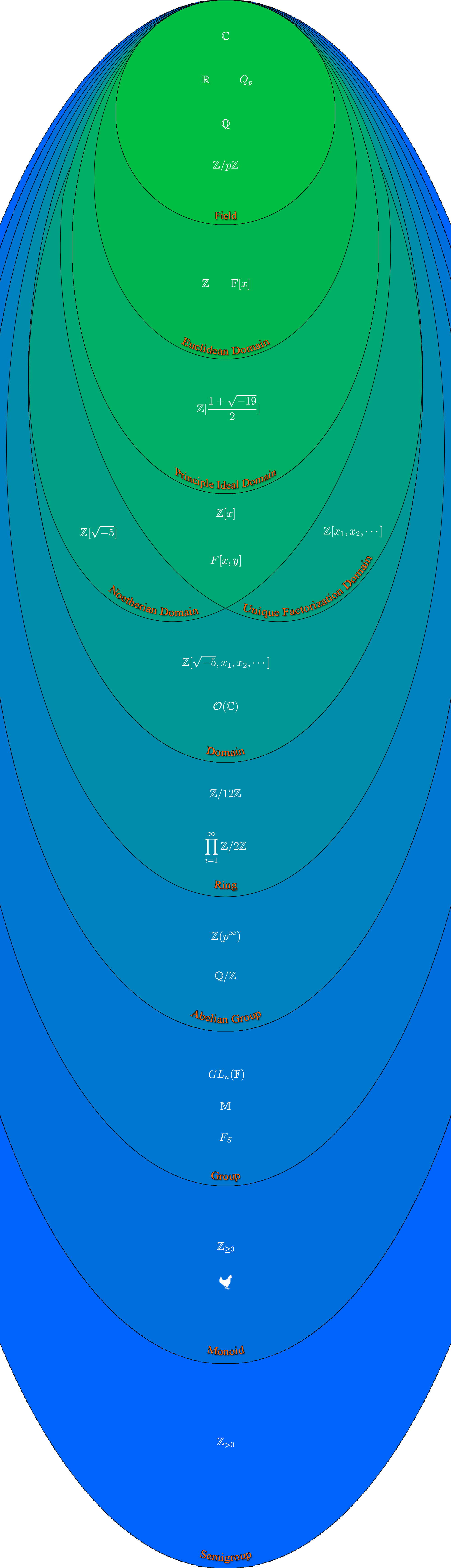
*Unfortunately, this picture can technically be misleading around the "Ring" and "Abelian Group" portion as it turns out every abelian group can have a ring structure attached to it if the law of composition is defined properly, it just might not be unital. For example, you can define multiplication to send everything to the additive identity. There are clearly no units, however, this will still meet all of the requirements to be a ring (depending on your definition of a ring). You can read more about it here and here. Some people like to use the term rng, pronounced "rung", to distinguish between rings without unit and rings with. Personally, I believe that nonunital rings should be categorized as rings and the almighty Hungerford, scripture for algebraists, doesn't require rings to be unital so therefore it must be true. That being said, I still decided to have separate classifications to distinguish the differences that we typically care about between the two algebraic objects.